#Project 1-조합회로로 루트계산기 만들기
앞서 설명한 루트계산기를 조합회로(combination logic)으로 구현해 보자. 조합회로로 주어진 모듈을 설계하려면 1 과정만에 결괏값이 나와야 한다. 즉 모듈에서 시퀀셜 한 과정이 이루어지면 안 되고 주어진 로직에서 한 번만에 연산이 이루어져서 출력값이 나와야 한다는 것이다. 따라서 로직합성과정에서 FF(플립플랍)를 생성해서는 안된다. 이러한 조건에서 한번 설계해 보자. 먼저 루트값을 계산하기 위해서는 소수 부분의 계산이 필수적인데 앞서 설명한 2가지 방법으로 소수계산을 진행해 보자. 필자의 경우에는 부동소수점 방법을 이용해 루트계산기를 설계하였다.
#설계의 과정
설계의과정은 루트값을 구하고, 구한 값의 근삿값을 결정하고, 근삿값을 변환해서 segment decoder를 통해서 변환하는 과정이다. 첫 번째 과정이 모듈설계구현의 핵심과정이다. 먼저 주어진 input에 대해서 부동소수점을 이용해 정규화를 해주는 과정이 필요하다. 따라서 코드 첫 번째 과정에서 다음과 같은 구문이 필수적이다.

10비트의 입력값을 받고 출력은 Q(5.3)이므로 총 8비트 출력값을 갖는 모듈이므로 in/out 포트비트수를 위와같이 맞춰준다. 특히 정규화의 과정을 위해서 입력값에 64를 곱해서 새로운 변수를 선언해 준다. 64를 곱하는 이유는 다음과 같다.
1. 64를 곱해 연산의 간략화
root(input)=output 에서 input은 10비트 입력값이고 출력값은 5비트 정수+3비트 소수이므로 총 8비트로 출력값이 정해진다. 따라서 수식상으로 root(0000000000)=xxxxx.xxx에서 우변의 소수 부분의 정규화를 해준다. 소수 부분이 3자리이므로 양변에 2^3을 곱하면 2^3*root(0000000000)=xxxxxxxx이 되는 것을 알 수 있다. 하지만 이 상태에서는 root식이 있으므로 코드상에서 실제로 구현하기에 힘들다. 따라서 root 식을 없애주기 위해서 같은 식을 곱해서 root를 소거시켜 준다. 쉽게 말해 등식을 제곱해서 root를 없애는 작업이 필수적이다. 따라서 다음과 같이 식이 성립된다.

다음과 같이 식이 간단하게 비교할 수 있는 수준으로 만들어진다. 이때 000000000은 우리가 입력한 입력값이고 xxxxxxxx은 우리가 근사해야 할 근삿값이다. 엄밀히 따지자면 등식은 틀린 것이다. 근삿값이므로 완전히 동일한 값은 아니기 때문이다. 하지만 2진수 특성상 정확한 값을 구할 수 없으며, 설령 구할 수 있다고 하더라도 지금의 방법보다 더 많은 비트수를 요구할 것임은 분명하므로 위와 같은 등식의 특성을 이용해서 비교식을 유도해서 사용하겠다. 비교식을 통해서 xxxxxxxx를 구하는 것이 모듈의 설계목적이다.
2. 정수부분의 결정
xxxxxxxx에서 상위 5비트는 정수부분인 것은 이해를 했을 것이다. 이제 if/else 비교문을 통해서 근삿값을 결정해야 하는데 처음부터 모든 정수 부분을 결정하면 비교 부분(경우의 수)이 많아져서 코드가 매우 길어지므로 근삿값의 정수 부분을 먼저 결정하고 근삿값을 결정하는 과정이 코드의 간결성에 좀 더 유리할 것이다. 루트값의 정수 부분을 결정하는 것은 별로 어렵지 않다. 어떤 수 k가 16~25이면(16 <k <25) k의 루트값은 4.xxx 인 것을 직관적으로 알 수 있다. 이와 같이 어떤 자연수가 제곱수사이에 위치한다는 사실을 이용해 루트값의 정수 부분을 쉽게 구할 수 있다.
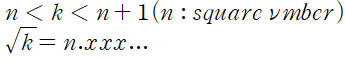
위의 원리를 코드상에서 구현하려면 if/else문을 여러 개 사용해서 입력값에 따라서 정수 부분이 결정될 수 있다.
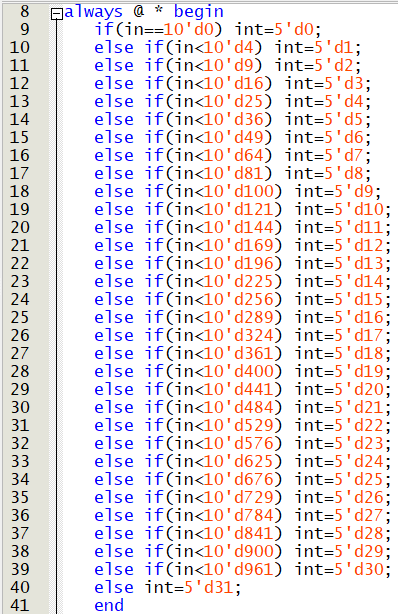
입력값이 10비트이므로 정수로는 1023이 입력될 수 있는 가장 큰 숫자임을 알 수 있다. 위의 코드처럼 입력값과 0~1023까지의 제곱수와 비교해서 근삿값의 정수 부분을 결정할 수 있다. 비교문의 개수는 0~1023까지의 제곱수의 개수이므로, 조합회로인 비교문으로 합성되는 것을 예상할 수 있다. 또한 입력값이 0~1023이므로 출력값의 정수는 0~31 임을 수학적으로 바로 알 수 있을 것이다.
3. 소수 부분의 결정
정수 부분을 앞선 코드를 통해서 5비트 바이너리로 결정한 뒤에, 이제는 소수 부분을 결정한다. 소수부분은 3비트이므로 총 2^3=8가지의 소수가 존재한다.
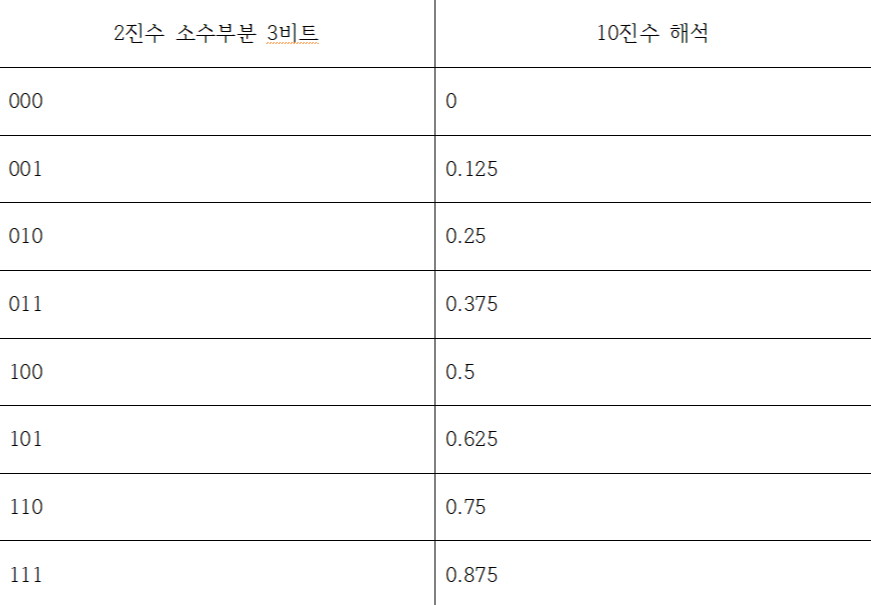
앞서 유도한 등식에서 소수 부분을 한번 결정해보자. 입력값에 64를 곱한등식은 64*input=(근사값(5비트정수+3비트소수))^2이다. 우리는 근사값을 구하는 모듈을 만드는것이 목적이다. 앞선 과정에서 5비트 바이너리 정수부분은 결정이 되었다. 따라서 설계자는 위 8가지 소수에 대해서 비교기를 설계해서 input에 64를 곱한값과 가장 비슷한 결과값을 찾는것이 핵심이다. 따라서 앞서구한 정수부분에 소수 000,001,010...을 붙여서 제곱을 하는과정이 필수적이다. 이때 우리가 구한 정수부분에 소수부분을 어떻게 붙일까? Verilog 에서 이러한 과정을 가능케하는 스킬이있다. 바로 concatenate이다. concatenation을사용하면 복잡한과정없이 바로 정수부분과 소수부분을 합칠 수 있을 것이다.

앞선구한 정수 부분에서 소수 000,001,010... 을 붙여서 제곱한 값을 remain1, remain2...로 assign 해준다. 따라서 각각의 remain값과 input*64의 값을 비교해서 input*64의 값과 가장 비슷한 remain의 값을 찾고 그 remain에 해당하는 소수가 결국 최종적인 근삿값의 소수 부분이다. 특히 remain9는 근삿값이 그다음 정수에 가까울수도 있기때문에 정의해준 값이다. 따라서 총 remain1~remain9까지 9가지의 경우가 존재한다. 다음정수로 넘어가는 경우를 예시를 한번 들어보자. 만약 근사값이 12.985일경우에는 12.875보다 13에 좀더 가깝다. 따라서 근사값은 12.875보다 13이 좀더 정확한 근사값이 된다. 이제 비교문을 통해서 가까운 근삿값을 최종적으로 결정해 보자.
4. 근삿값의 비교과정

위와 같이 비교문을 통해서 가장 가까운 근삿값을 구할 수 있다. 만약 input*64의 값이 remain1~remain2에 위치하는경우 input*64의값이 remain1과 remain2중에 어떤 값에 좀 더 가까운지 비교문안의 비교문으로 판단한다. squ=input*64로 취급해서 각각의 remain값과 비교한다. 특히 마지막 비교문을 주목해 보자. 소수 부분이 0.875 이상일 때 0.875와 그 다음정수를 비교하는 명령문이 들어가 있다. 하지만 만약 입력값의 정수 부분이 31이라면 출력값은 32가 될 수 없으므로 무조건 31.875로 근사해야 오류가 생기지 않는다. 왜냐하면 설계결과는 2개의 hex16진수로 표현되어야 하기 때문에 32는 표현될 수 없는 출력값이기 때문이다. 따라서 각 비교문 밑에 result로 최종결과값은 int(결정한 정수 부분) 5비트+비교문을 통한 case별 소수(000,001,010...)로 최종적으로 8비트 출력값이 나오는 것을 확인할 수 있다.
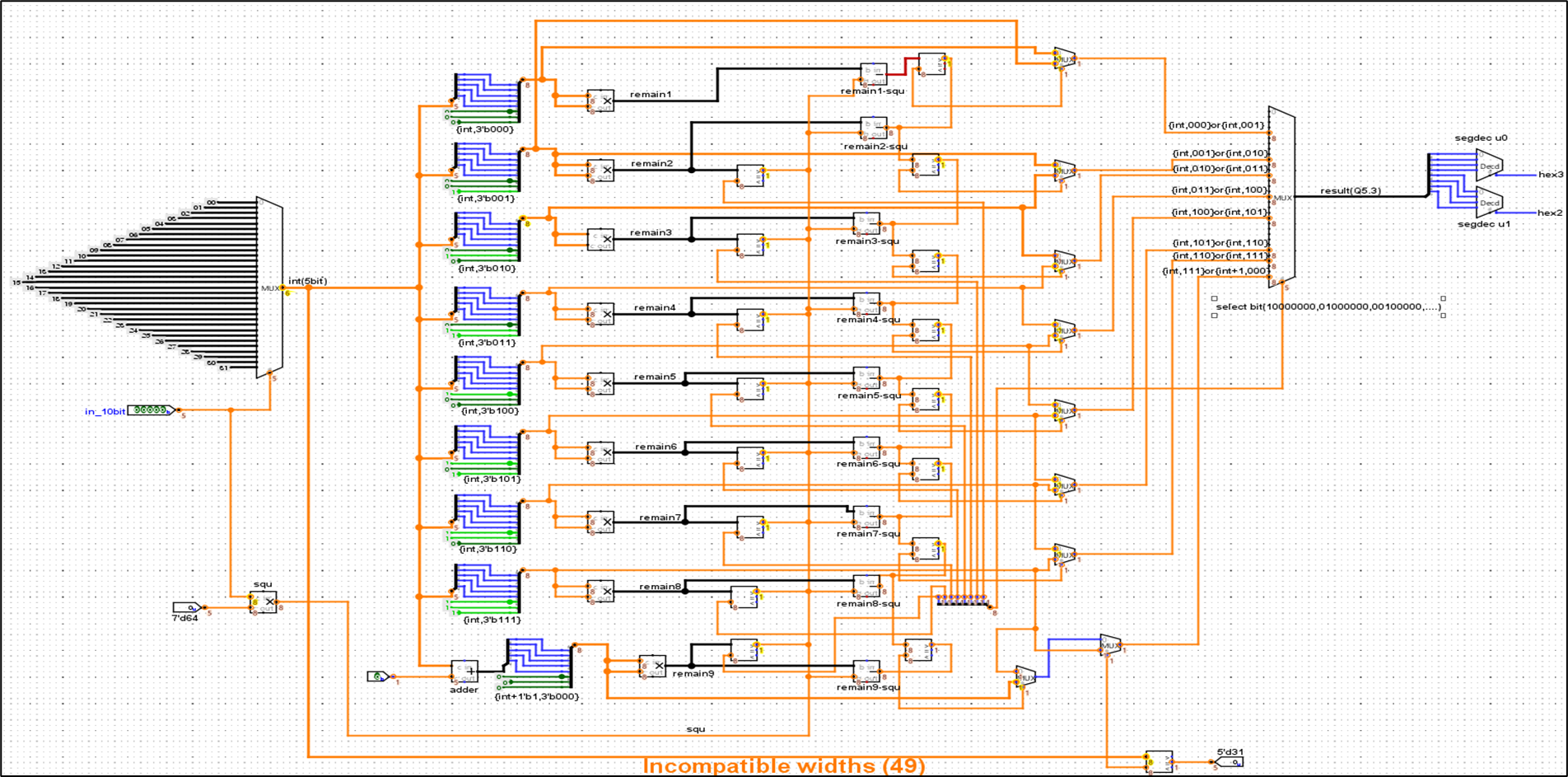
스키매틱을 그려보면 다음과 같이 비교기와 mux로 표현되는것을 확인할수있다. 로직의 갯수가 많아서 다소 복잡해보일수있지만 코드의 구조를 이해하고 다시 보면 그렇게 어렵진않다. 스키매틱에서 사용된 로직은 mux,adder,비교기,곱셈기,뺄셈기 등이 사용되었다. 실제로 코드에서 RTL-simulation을 통한 합성과는 다르지만 코드가 합성한 RTL스키매틱은 매우 복잡하고 로직의 갯수가 많으므로 간단하게 나타내었다.
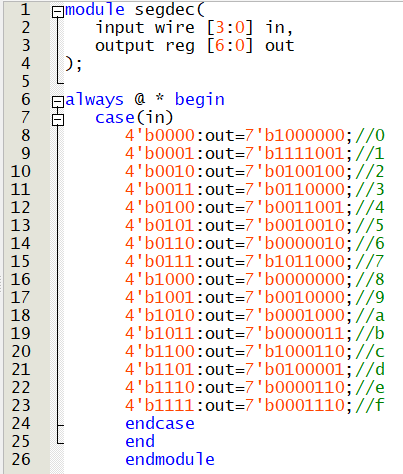
위와 같이 세그먼트 디코더를 인스턴스 해서 최종적인 결괏값을 출력한다.
'Project > DSD project' 카테고리의 다른 글
| [Project] Verilog Term Project-2차방정식 (0) | 2023.01.14 |
|---|---|
| [Project] Verilog Term Project-루트계산기(3) (0) | 2023.01.13 |
| [Project] Verilog Term Project-루트계산기(1) (0) | 2023.01.08 |


