전자기학이라는 학문을 이해하고 공부하기 위해서는 벡터의 표현과 이해가 필수적이다. 특히 벡터의 표현은 좌표계마다 달라지는데, 우리는 이 좌표계별로 벡터표현을 익혀야 할 필요성이 있다. 전자기학에서는 우리에게 익숙한 직교좌표계뿐만 아니라 원통좌표계, 구좌표계등 다양한 좌표계가 존재한다. 이렇게 다양한 좌표계가 존재하는 이유는 다양한 전기적인 상황을 이해하는 데에 직교좌표계보다 다른 좌표계를 사용하는 것이 더 유리한 상황이 존재하기 때문이다. 따라서 이러한 다양한 좌표계 역시 알아야 할 필요성이 있다.
#벡터의 표현
벡터는 알다시피 크기와 방향을 가지는 물리량이다. 속도와 속력이 다른것처럼 벡터와 스칼라는 확연히 다르다. 따라서 벡터를 표현할 때는 벡터라고 표시해야 한다.

위와 같이 벡터를 표시할 수 있다. 고등과정에서 배웠던 것처럼 위에 화살표로 표현할 수도 있고 첨자를 이용해서 표현할 수도 있다. 표현의 차이일 뿐이지 벡터라는 의미는 동일하다.


특히 단위벡터가 많이 사용되는데, 단위벡터는 크기가 1인 벡터를 말한다. 다시말해 크기를 1로 만들고 오직 방향만을 내포하는 값으로 만들어준 것이 단위벡터이다. 이제부터 벡터를 표현할 때 이 단위벡터를 이용해서 표현한다. 왜냐하면 일반벡터를 사용하면 방향과 크기모두를 내포하고 있기 때문에 연산할 때 구분해서 연산하기 힘들기 때문이다. 따라서 다음과 같이 표현한다.

위와 같이 크기와 단위벡터의 곱으로 벡터량을 표현한다. 후에 적분연산이나 다양한 연산에서 크기와 벡터를 따로 취급할 수 있기 때문에 위와 같이 단위벡터를 사용해서 표현하는 것이 매우 유리하다.
#벡터의 내적과 외적
벡터는 크게 2가지의 연산자를 포함한다. 내적은 연산결과가 스칼라가 되고 외적은 연산결과가 벡터이다. 먼저 내적부터 알아보자.

벡터의 내적연산은 위와같이 정의된다. 벡터 a와 벡터 b를 내적 하면 각각의 크기를 곱하고 각 벡터가 이루는 각의 코사인값을 모두 곱한 결과가 내적값이다. 따라서 내적의 연산에서 벡터가 없기 때문에 연산결과는 벡터가 아닌 스칼라가 되는 것이다. 특히 내적이 가지는 물리적인 의미는 정사영의 개념이다. 정사영은 말 그대로 벡터의 그림자를 의미한다.
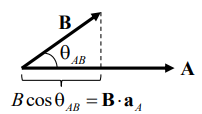
위와 같이 정사영의 개념이 곧 내적의 개념이므로 어떤 내적연산이 있을 때 정사영의 개념으로 대체될 수 있다. 특히 내적연산의 의미는 특정방향의 단위벡터와 내적을 했을 때 그 방향의 스칼라값이 나온다는 것에서 의미가 있다.
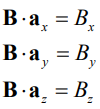
어떤 특정벡터 B벡터를 각 방향별로 내적하게되면 B벡터의 방향성분이 결괏값으로 나오게 된다. 이는 내적의 가장 중요한 성질이며 방향성분을 구하는 과정으로 많이 사용되는 개념이므로 꼭 알아두어야 한다. 후에 적분을 하는 과정에서도 많이 사용되는 연산이다. 그다음 외적에 대해서 알아보자. 내적과는 달리 외적연산은 연산결과가 벡터가 되는 연산이다.

벡터의 외적은 오른손 법칙을 따른다. a벡터와 b벡터를 외적하면 a에서 b를 오른손으로 감싸서 쥔방향의 엄지손가락 방향이 외적 한 결과벡터의 방향이다. 외적의 크기는 두 벡터가 이루는 평행사변형의 면적이 크기이다. 벡터의 외적은 연산을 해서 새로운 벡터를 만들어 내는 데에 의미가 있다. 특히 면적에 대한 법선벡터를 처리할 때 자주 사용되는 개념이므로 잘 알아두자.
'전공 > 전자기학1' 카테고리의 다른 글
| [전자기학1] 구좌표계 (0) | 2023.02.24 |
|---|---|
| [전자기학1] 원통좌표계 (0) | 2023.02.24 |

