이전에 소개했던 square wave형태인 전위 함수에 각영역에 따라서 슈뢰딩거 파동방정식에 적용하면 다음과 같다.

주기적인 결정은 가진 원자구조에서의 파동함수는 주기성을 가진다는 블로흐의 정리를 이용해서 파동함수의 기본적인 형태를 정의하고 파동방정식에 대입해 보자. 특히 3차원 파동방정식에서 1차원 파동방정식으로 차원을 낮출필요가있다.


1 영역에서는 v=0이므로 슈뢰딩거 파동방정식이 간단한 형태로 바뀌게 된다. 따라서 2계 미분방정식의 형태로 나오게 되며 특성방정식을 통해서 일반해를 결정한다.
하지만 2 영역에서는 v가 0이 아니기 때문에 좀 더 복잡한 식의 형태를 가진다. 두 상황에서 모두 일반해를 결정하고 경계조건을 적용해서 해를 결정할수 있다.

따라서 경계조건을 적용한 식에 좀더 해결가능한 식으로 만들어주기 위해서 수치해석방법을 이용해서 식을 정리하면 다음과 같이 최종식이 나온다. 이 식에서 전위장벽이 있을 때와 없을 때의 경우를 나누어서 식을 해석해 보자. 전위장벽이 없을 때(V=0)는 자유전자에 해당하고 전위장벽이 있을 때는 구속된 전자를 의미한다.
#전위장벽에 따른 Diagram 형성


특히 전위가 0이 아닐 때를 주목해 보자 f함수가 코사인함수이므로 범위가 -1,1의 사이에 있기 때문에 그래프상에서도 가능한 값들이 제한된다.

그래프상에서 a, b, c, d로 구간이 나타나는데, b, c구간은 1,-1을 벗어나는 구간이므로 전자가 존재할 수없다. 따라서 주기성에 의해서 다음과 같이 e-k다이어그램이 나온다.
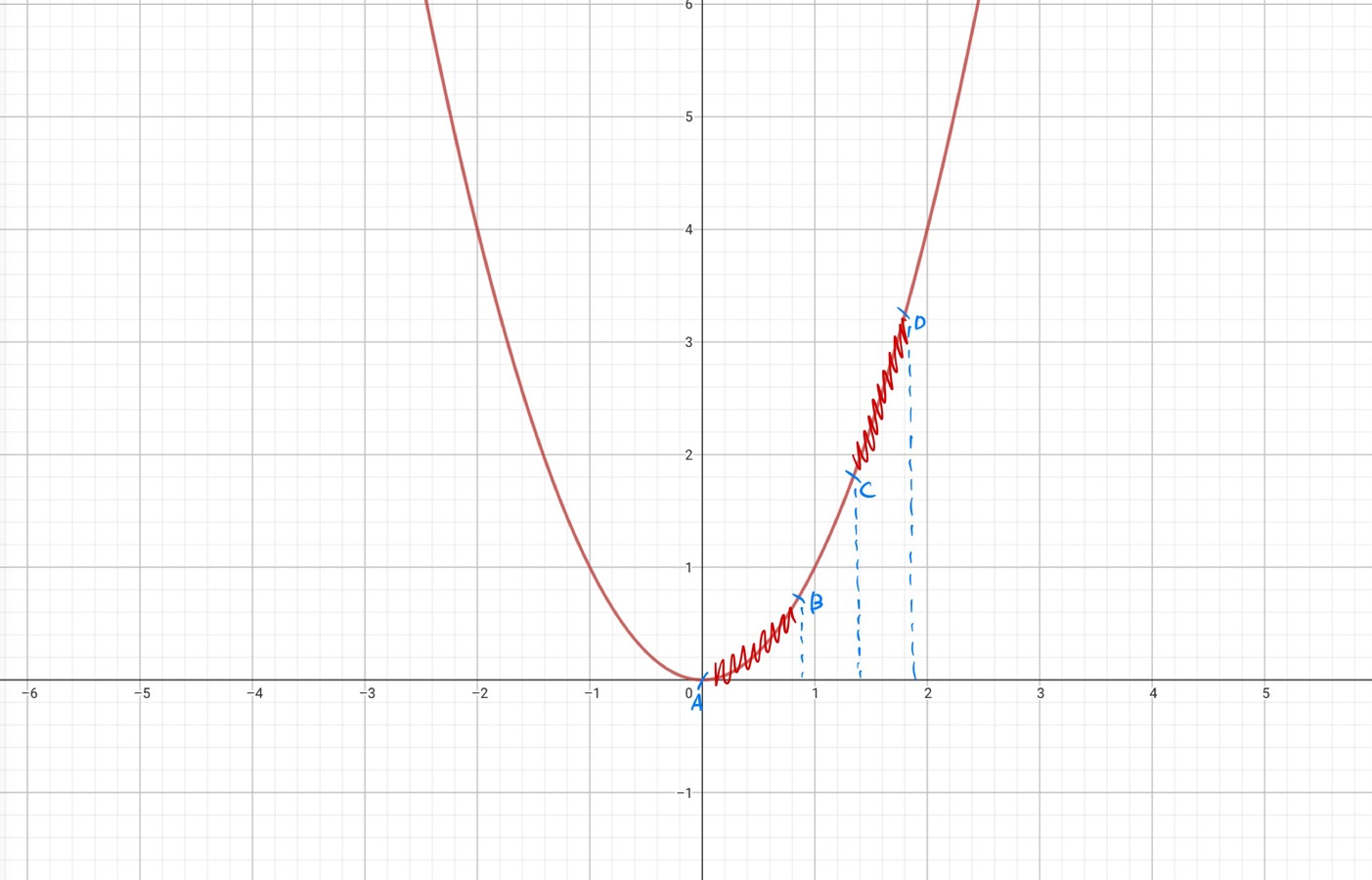
자유전자의 e-k다이어그램에서 구간을 동일하게 표시해 보자. b-c구간은 전자가 존재할 수 없으므로 그래프가 잘릴 것이다. 그래프가 잘린다는것은 특정영역에서 전자가존재하지 않는다는것이고 함수는 주기성을 가지므로 존재할수없는 구간이 매우많을것이다. 따라서 이 결과는 특정 구간에 전자가 존재하지 못하는 밴드갭(band gap)의 존재를 증명해주는 것이다.
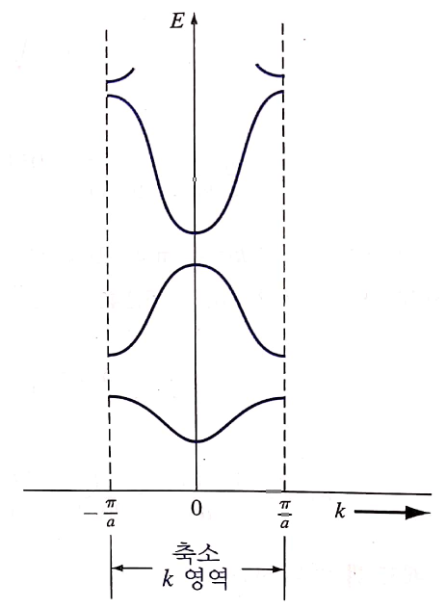
앞서 짤린 그래프들은 주기성을 가지기 때문에 한 주기로 축소할 수 있다. 따라서 한 주기에서 모두 이어 붙이면 다음과 같이 함수분포가 나타나는데 이는 전자의 밴드분포로 취급될 수 있다. 즉 함수들 위아래의 간격이 결국 밴드갭이 되는 것이다. (전자가 존재할 수없으므로)
'전공 > 물리전자' 카테고리의 다른 글
| [물리전자] 페르미-디랙 확률함수(Fermi-Dirac probability function) (0) | 2023.01.31 |
|---|---|
| [물리전자] 상태밀도함수(Density of state function) (0) | 2023.01.31 |
| [물리전자] The K-space Diagram (0) | 2023.01.20 |
| [물리전자] 에너지밴드(Energy band) (2) (2) | 2023.01.19 |
| [물리전자] 에너지 밴드(Energy band) (0) | 2023.01.19 |



