지금까지는 에너지밴드의 정의와 밴드가 어떻게 형성되는지 알아보았다. 하지만 여전히 밴드 내에서 전자가 어떻게 움직이고 어떤 역학을 형성하는지 알지 못한다. 우리는 반도체소자의 전류-전압특성과 전자의 이동에 관심이 있기 때문에 형성한 밴드 내에서 전자가 어떻게 움직이고 형성하는지를 알아내는 것이 최종목표이다. 따라서 이번에는 캐리어의 움직임과 농도를 파악하기 위한 상태밀도함수에 대해서 한번 알아보자.
상태밀도함수란 말그대로 상태밀도를 함수로 나타낸 것이다. 한상태에는 하나의 전자가 위치할 수 있으며 전자가 위치할 수 있는 자리밀도를 함수로 쉽게 나타낸 것이라고 생각하면 될 것이다.
#상태밀도함수 유도

먼저 3차원전위우물을 가정해서 슈뢰딩거 파동방정식에 주어진 함수를 대입해서 방정식을 푼다. 마찬가지로 3차원 파동함수는 3개의 미지수가 존재하므로 3변수분리법을 이용해 각각의 파동함수를 푼다. 각 변수에 대해서 일반해를 결정할 수 있다.

앞서 구한 일반해에서 0과 a에서 경계조건을 적용한다(자연상태의 파동함수는 연속이다.) 따라서 k파수벡터가 각 변수에서 유도된다. 차원관계식의 정의를 이용해서 각각의 방향벡터식에 대해서 식을 유도할 수 있다. 특히 Kx+1-Kx의 식은 각 방향에서의 양자상태거리를 의미한다. 따라서 3방향거리를 곱한것은 한 양자상태가 가지는 부피가 된다.


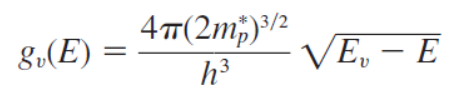
마지막으로 파수벡터와 에너지관계식을 통해서 미분식을 유도하고, 상태밀도함수를 유도할수있다. g(k)에 대한 식을 좀 더 알아보면 2는 스핀양자수가 2개이므로 2를 곱한 것이고, 1/8은 공간상태가 8개 중에 한 개로 취급되기 때문에 1/8을 곱한 것이다. 그리고 분모는 밀도이므로 한양자상태가 가지는 부피로 나누어준 것이다. 분자는 공간에서의 미소부피식이 들어간다.
이식을 각각 밴드에서 적용하면 범위에 따라서 루트안의식이 반대로 되면서 항상 양수인 값이 된다.

그래프를 분석해 보면 컨덕션 밴드에서는 거리가 클수록(에너지가 클수록) 자유전자의 상태밀도가 점점 커지는 것을 알 수 있고, 밸런스 밴드에서는 거리가 작아질수록(에너지가 작아질수록) 양공의 상태밀도가 점점 커진다고 해석할 수 있다.

그래프의 해석이 헷갈린다면 컨덕션밴드와 밸런스밴드 경계에서 가장 많은 전자와 양공이 존재한다고 생각하자 그러면 전자자리는 컨덕션밴드에서 멀어질수록 더 많이 존재할 것이고 양공자리는 밸런스밴드에서 멀어질수록 더 많이 존재할 것이다. 하지만 두 밴드에서 멀어지는 방향은 반대이므로 전자는 에너지가 커지는 방향, 양공은 에너지가 작아지는 방향으로 비례한다.
'전공 > 물리전자' 카테고리의 다른 글
| [물리전자] 평형상태의 캐리어분포(Charge carriers in semiconductors) (0) | 2023.02.01 |
|---|---|
| [물리전자] 페르미-디랙 확률함수(Fermi-Dirac probability function) (0) | 2023.01.31 |
| [물리전자] The K-space Diagram (2) (0) | 2023.01.28 |
| [물리전자] The K-space Diagram (0) | 2023.01.20 |
| [물리전자] 에너지밴드(Energy band) (2) (2) | 2023.01.19 |



