이전에는 전자가 가지는 양자상태함수에 대해서 알아보았는데 이번에는 전자가 존재할 수 있는 확률에 대한 함수를 한번 알아보자. 즉 이전에는 g(E)의 함숫값은 양자상태(state)이고 이번에 배울 페르미-디랙 확률함수는 f(E)의 함숫값은 확률이다. 따라서 항상 0~1 사이의 값을 가지게 된다. 이러한 확률함수를 도입하는 이유는 전자의 입자는 매우 작고 움직임 또한 매우 빠르기 때문에 우리가 확실하게 위치와 운동량을 결정할 수 없다. 따라서 확률을 도입해서 근사적으로 이 위치에 전자가 존재할 확률은 ~%이다라고 해석해서 전자의 역학을 관찰한다.
#페르미 디랙 확률함수 유도

특정 에너지 준위 Ei에서 순열의 개념을 이용해서 일반화 한뒤에 전자는 모두 같다고 취급하고 전자개수의 팩토리얼을 나누어준다. 따라서 특정에너지 준위에서 전자가 배열되는 총경우의 수를 구할 수 있다.

각각의 에너지준위는 독립적인 시행이므로 곱해서 총경우의 수를 표현할 수 있다. 이를 근사하기 위해서 스털링근사를 통해서 해석한다. 에너지레벨은 매우 큰수이므로 스털링근사가 적절하게 적용될수있다. 그다음 식을 간단히 하기위해서 라그랑주 승수법을 이용해 exp 식을 유도해서 전자의 존재확률식을 유도한다.
#페르미 준위(Fermi Energy level)
유도한 확률함수를 나타내기위해서 페르미에너지 준위라는 개념을 도입해야한다. 페르미 준위는 정의를 2가지 입장에서 내릴수있다. 절대영도(0K)에서 전자가 가질수있는 최대 에너지 준위로 정의될수있고, 또한 임의의 온도 T에서 전자가 채워질 확률이 1/2인 지점을 페르미에너지 준위라고 정의한다. 간단하게 생각해 페르미 확률함수의 기준이 되는 기준 point라고 생각하면 된다. 함수개형은 이 준위를 기점으로 대칭구조를 이루고 있으며 온도가 높아질수록 전자들이 에너지를 받아 이 페르미 준위보다 더 높은 레벨을 가질수있다는것을 의미한다.

따라서 결론적으로 다음과 같이 확률함수의 식이 최종적으로 유도된다. 이 함수는 온도에 대해서 다른 그래프형태를 가지는데 먼저 0k일 때와 0보다 큰 k일 때의 경우를 그래프로 한번 알아보자.
1. 0K일 때


온도가 0K일 때는 사실상 분모에 0이 들어가게 되므로 수학적으로는 정의되지 않지만 물리적으로는 매우 간단하다. 온도가 매우 낮을 때는 입자의 운동이 거의 없으므로 페르미에너지준위를 기점으로 존재하거나, 존재하지 않거나 둘 중의 하나의 상태를 가지게 된다. 따라서 무조건 0과 1의 확률을 가지며, 그사이 확률은 가지지 않는다는 특징을 가진다. 따라서 페르미에너지 준위보다 낮은 상태에서는 100%로 전자가 존재하고 페르미에너지보다 높은 상태에서는 전자가 존재하지 않는다.
2. 0K보다 높을 때


온도가 0k 이상일 때는 입자의 운동이 존재하기 때문에 확률이 0과 1이 아닌 다른 확률이 존재한다. 따라서 페르미 에너지레벨을 기준으로 전자들이 좀 더 다양하게 분포하기 시작한다. 하위레벨에서 상위레벨로 전이되는 전자도 존재하는 반면, 상위레벨에서 하위레벨로 전이하는 전자도 있을 것이다. 다양하게 전자들이 전이되기 때문에 확률 역시 페르미레벨부근에서 가장 변동이 크다. 온도가 높아질수록 그래프의 개형 역시 확률이 더 많이 벗어나는 방향으로 형성된다.
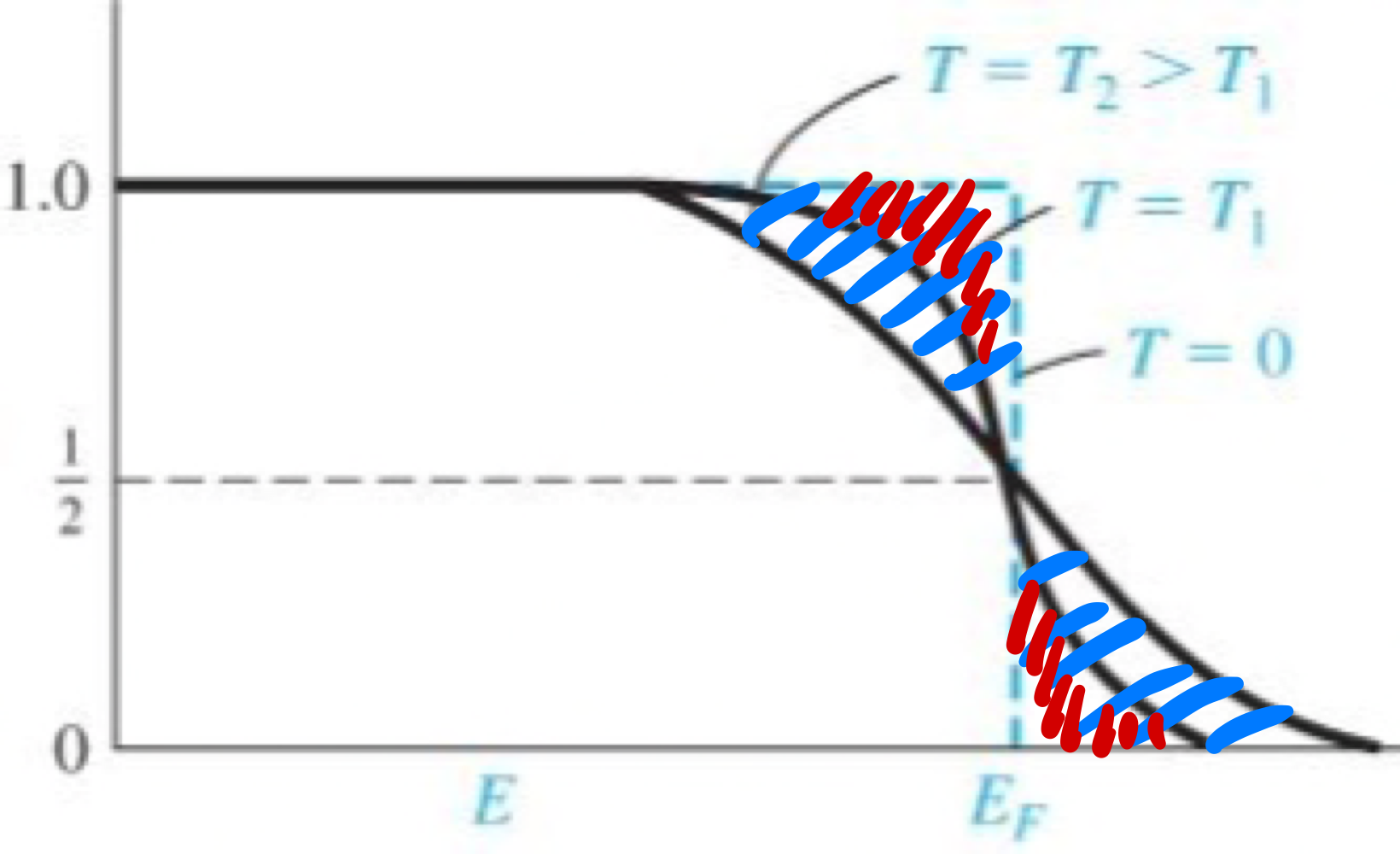
확률함수는 페르미 에너지 준위를 기준으로 좌우측 함수의 넓이가 같다. 왜냐하면 전자가 없어진 만큼 상위에너지에서 존재하기 때문에 왼쪽 비어있는 넓이와 오른쪽 채워진 함수 부분의 넓이가 같다는 것을 꼭 인지하자. 위 그래프에서도 같은 색으로 표시된 부분이 넓이가 같은 부분이다.
#Maxwell-Boltzmann 근사
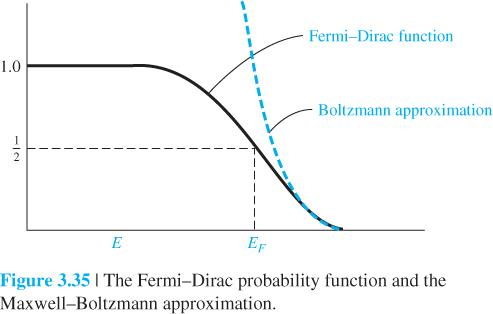
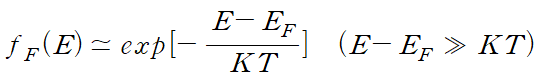
페르미 디랙함수는 확률을 단일적으로 구할 때는 많이 사용되지만 후에 적분식에서는 많이 사용되지는 않는다. 왜냐하면 페르미 디랙함수는 적분이 힘든 형태로 되어있어서 실제로 활용되는데 약간의 한계가 있다. 따라서 적분식에는 멕스웰 볼츠만 근사식을 이용해서 적분이 가능한 형태로 만들 수 있다. 볼츠만 근사식에서 E-Ef가 항상 KT보다 매우 커야 근사식이 성립한다는 것을 항상 기억하자. 후에 적용하는 거의 모든 식이 이 볼츠만 근사식이 적용된다는 조건하에 유도되는 식이기 때문에 꼭 조건을 기억하도록 하자.
'전공 > 물리전자' 카테고리의 다른 글
| [물리전자] 진성 캐리어 농도(The intrinsic Carrier Concentration) (0) | 2023.02.01 |
|---|---|
| [물리전자] 평형상태의 캐리어분포(Charge carriers in semiconductors) (0) | 2023.02.01 |
| [물리전자] 상태밀도함수(Density of state function) (0) | 2023.01.31 |
| [물리전자] The K-space Diagram (2) (0) | 2023.01.28 |
| [물리전자] The K-space Diagram (0) | 2023.01.20 |



