이번에는 회로 단순화 기법 중에 가장 중요한 테브냉 등가회로에 대해서 한번 알아보자. 테브냉 등가회로는 회로 단순화 기법이고 회로전체에 대한 해석보다 한 단자에 대해서 해석을 할 때 유용하게 사용되는 기법이다. 특히 복잡한 회로구성을 전압원과 저항이 직렬로 연결된 단순회로로 바꿀 수 있다는 점에서 의미가 있다. 먼저 기본적으로 사용되는 개념부터 알아보자.
#회로의 단락과 개방(Short/Open)
-Short(단락)
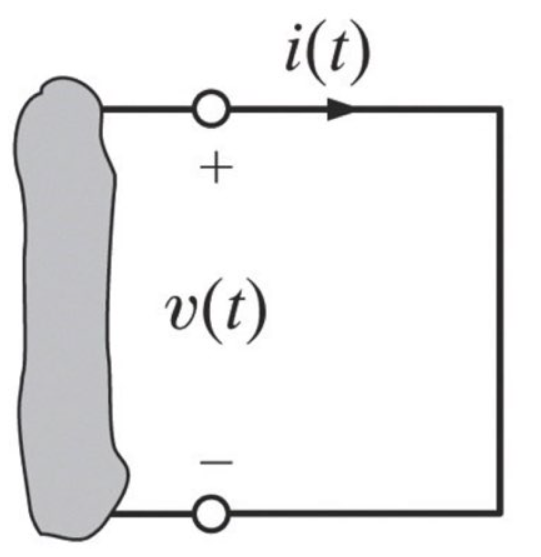
회로의 단락은 어떤 소자(저항)없이 단순하게 선으로만 연결되어 있는 상태를 단락상태라고 정의한다. 이때 단락된 지점의 모든 부분은 전위가 동일하기 때문에 전압강하가 존재하지 않는다.(소자가 존재하지 않으므로) 따라서 단락 부분의 전위차는 0이다. 하지만 단락 된 부분에서 도선이 연결되어 있기 때문에 전류는 흐를 수 있다.

옴의 법칙을 이용해 좀더 수식적으로 접근해 보면 도선의 내부저항이 0이라고 가정하면 단락 된 부분의 저항은 0이 된다. 따라서 저항이 0이므로 전위차는 0 임을 알 수 있다.
-Open(개방)

회로의 개방은 도선이 단선이 되어있는 상태를 말한다. 말 그대로 도선이 단선되어서 회로가 끊어져있는 상황을 개방상태라고 하며, 이때 회로에는 전류가 흐르지 않게 된다. 단선되어 있다는 것은 전류가 흐르지 않는다는 것을 의미하며 이는 곧 저항이 무한대의 값을 갖는다는 것과 동일한 상황이다. 전류는 흐르지 못하지만 주어진 회로 따라서 전위차는 존재할 수 있다. 왜냐하면 단선된 부분의 위쪽노드와 아래쪽노드가 다른 노드이기 때문에 전위차가 충분히 생길 수 있을 것이다.

옴의 법칙을 이용해서 마찬가지로 나타낼 수 있다. 전류와 저항의 관계식에서 저항이 무한대의 값을 가지므로 전류는 거의 흐르지 않게 된다.
#테브냉 등가회로
앞서 설명한 대로 테브냉 등가회로는 복잡한 회로를 한 소자에 대해서 전압원과 저항으로 직렬연결된 회로로 단순화할 수 있는 기법이라고 설명했다. 테브냉 등가회로로 간단화하는 작업은 한 가지 방법이 아닌 여러 가지 방법이 존재하는데 회로마다 유리한 방법을 적용하는 것이 단순화 작업을 하는데 많이 유리하다.
1. 테브냉 전압과 단락 회로전류를 구하는 방법

a-b노드를 기점으로 테브냉 전압을 먼저 구해보자. 전압을 이때 a-b는 개방상태이므로 전류가 흐르지 않는다. 따라서 4옴 저항 역시 전류가 흐르지 않게 되어 전압이 걸리지 않으므로 현재 회로를 해석하는 데에 있어서 영향이 없다는 사실을 알아야 한다. 따라서 다시 회로를 그려보면

앞서 설명한 노드방법을 이용해서 테브냉 전압을 바로 구할 수 있다. 이어서 단락회로전류를 구해보자.

방금과는 다르게 단락회로전류를 구하기 위해서 a-b를 단락 시키고 전류를 구해야 한다. 따라서 4옴의 저항은 전류가 흐르게 되어 회로영향이 생기므로 따로 고려해주어 한다. 마찬가지로 v2에 대한 전압방정식을 세워서 전압을 구하고 isc를 구한전압을 이용해서 회로전류를 구할 수 있다.


앞서 구한 테브냉전압과 단락전류를 옴의 법칙을 이용해서 테브냉 등가저항을 결정할 수 있다. 따라서 등가저항은 8옴이 이므로 다음과 같이 테브냉 등가회로가 32V 전압원과 8옴 저항 등가저항으로 단순화되었다.
2. 등가저항을 먼저 결정하는 방법


위와 같은 회로로 예시를 들어보자. 회로의 구조를 보고 등가저항을 구하기 쉽다고 판단되면 전압원은 단락 시키고, 전류원은 개방시켜서 저항만 회로에 남기게 한다. 그다음 단자에 대해서 바라본 등가저항을 계산한다. 위 회로는 a-b단자에 대해서 5옴과 20옴 저항은 병렬연결되어 있고 4옴은 직렬연결되어 있으므로 등가저항은 최종적으로 8옴이 된다. 따라서 테브냉 전압과 저항을 결정해서 회로를 단순화할 수 있을 것이다.
3. 테스트 전압원을 이용하는 방법

회로 소자에서 전압원과 전류원이 모두 종속일 때는 항상 테브냉 등가 전압원이 존재하지 않는다. 즉 테브냉 등가 전압이 0이다. 왜냐하면 실질적으로 만드는 전압이 없기 때문에 등가회로에서 등가전압원 또한 존재하지 않는다. 따라서 이 상황에서는 일반적인 방법을 사용해서 테브냉 등가회로를 구할 수 없고, 테스트 전압원을 이용해서 테브냉 등가 저항을 구해야 한다.
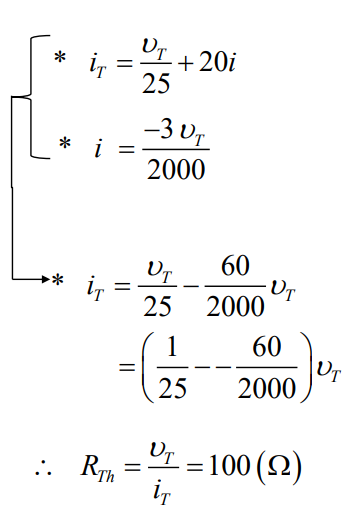
마찬가지로 노드방법을 이용해서 식을 유도한다. 하지만 테스트전압과 전류를 모두 값을 구하지 않고 식을 통해서 비를 구한다. 왜냐하면 어차피 테브냉 등가 저항의 값만 알면 되기 때문에 각각의 값을 모두 구할 필요 없이 저항만 구해서 등가회로를 간단히 나타낼 수 있을 것이다.
'전공 > 회로이론' 카테고리의 다른 글
| [회로이론] 연산증폭기(op amp) (0) | 2023.01.30 |
|---|---|
| [회로이론] 망전류해석법(Mesh-Current method) (0) | 2023.01.27 |
| [회로이론] 마디해석법(Node-Voltage method) (0) | 2023.01.27 |
| [회로이론] 회로망의 기본해석 (0) | 2023.01.27 |



