이번에는 2계 비제차상미분방정식에 대해서 한번 알아보자. 이전까지는 모두 우변이 0인 제차형태인 상미분방정식을 다루었는데 만약 0이 아닌 비제차형태인 상미분방정식일 경우에는 어떤 식으로 방정식을 풀어야 하는지 한번 알아보자.

위와 같이 일반적인 형태로 나타낼 수 있는데 이 형태에서 r(x)가 0이 아닌 경우가 비제차형태의 상미분방정식이라고 정의할 수 있다. 이때는 제차해와 비제차해에 대한 경우를 나누어서 구해야 한다. 즉 모든 경우에 대한 해를 구한 뒤에 중첩의 원리를 적용해서 일반해를 결정할 수 있다는 의미와 동일하다.
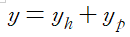
y의 일반해가 제차해+비제차해로 나타날 수 있고 이를 정의하기 위해서는 당연하게도 제차해와 비제차해를 모두 구해서 일반해를 결정해야 한다. 제차해는 우리가 저번에 배웠던 여러 가지 방법들로 구할 수 있을것이고 비제차해를 구해야 하는데, 비제차해를 구하는 방법은 크게 두가지가 있다. 미정계수법과 매개변수법을 이용해서 비제차해를 구할수 있다.
이번에는 미정계수방법에 대해서 한번 알아보자
미정계수방법은 0이 아닌 r(x)항이 어떤 함수냐에 따라서 비제차해에 대한 가설해를 세우는 것이 일반적인 방법이다.

동일하게 비제차해역시 주어진 미분방정식에 대입하면 성립해야 하기 때문에 계수들을 모두 결정할 수 있다. 즉, r(x)의 형태에 따라서 비제차해의 형태를 표에 나타난 대로 적절하게 선택하고, 각형태에 존재하는 미정계수들을 주어진 미분방정식에 대입해서 찾아가는 방법이 미정계수방법이다. 당연하게도 r(x)와 비제차해의 함수형태는 같은 미분방정식에서 나온 것이기 때문에 형태가 동일하다.
예제를 한번 풀어보자.

1. 제차해 구하기
좌변에 존재하는 y의 계수가 상수계수 이므로 특성방정식을 이용한다.

앞서 설명한 방법을 이용해 제차해의 일반해를 결정
2. 비제차해 구하기

주어진 r(x)가 지수함수 형태이므로 비제차해의 형태를 지수형태로 설정한다. 그다음 가설해를 주어진 미분방정식에 대입해서 계수를 결정하면 비제차해를 구할 수 있다.
3. 최종해 결정

따라서 최종적으로 해는 제차해와 비제차해의 합으로 나타난다.
'전공 > 공학수학' 카테고리의 다른 글
| [공학수학1] Laplace Transform (1) (0) | 2023.01.06 |
|---|---|
| [공학수학1] 2계 비제차상미분방정식 (2)-매개변수법 (0) | 2023.01.06 |
| [공학수학1] 2계 제차상미분방정식(3)-오일러 코시 방정식 (0) | 2023.01.05 |
| [공학수학1] 2계 제차상미분방정식(2) (0) | 2023.01.05 |
| [공학수학1] 2계 제차상미분방정식(1) (0) | 2023.01.05 |



