이번에는 라플라스 변환에 대해서 한번 알아보자. 지금까지 소개했던 내용들은 모두 미분방정식의 풀이법에 대한 설명을 했다. 하지만 이번에는 '변환'이라는 초점에 맞추어서 한번 개념을 정리해 보자. 지금까지 했던 내용들과는 많이 다른 내용이므로 개념과 정의를 먼저 소개하겠다.
1. 라플라스 변환의 개념
우선 라플라스 변환은 공학에 있어서 매우 중요한 의미를 가진다. 변환의 목적은 보다 복잡한 고계 미분방정식의 풀이에있다. 하지만 고계 미분방정식은 앞서 설명한 방법을 사용해도 복잡하지만 풀 수는 있다. 그럼에도 라플라스 변환이 공학에서 중요한 이유는 다음과 같다. 첫 번째로 보다 직접적으로 문제를 해결할 수 있다. 이전에 배웠던 방법은 제차해를 먼저 구한 다음에 형식에 맞추거나 공식을 사용해서 비제차해를 구해서 최종해를 구한 뒤, 초기값을 대입해서 특수해를 찾는 방법이다. 하지만 라플라스 변환을 이용하면 이러한 과정 없이 바로 변환해서 해를 구할 수 있다. 두 번째로 공학에서 자주 사용되는 불연속함수나 미분불가능한 함수들에 대한 해석을 좀 더 의미 있게 만들어 준다는 것에서 이 라플라스 변환은 매우 유용하다고 볼 수 있다.
라플라스 변환을 간단하게 설명해보자면 't영역에서 s영역으로 변환하는 과정'이라고 설명할 수 있겠다.

위와 같이 라플라스 변환을 정의할 수 있다. 적분변수가 t이므로 적분의 결과는 더 이상 t대한 값이 나오지 않고 s에 대한 함수로 결과가 나올 것이라고 직관적으로 알 수 있다.(t에 대한 정적분값이므로) 이때 f(t)에서 변수 t는 시간축을 의미하며, f(t)는 시간에 따른 어떤 특정값의 함수라고 정의될 수 있다. 여기서 f(t)는 적분값이 존재하는 유한함수임을 가정해야 함을 인지하자.

일반적으로 라플라스 변환후의 식을 대문자로 표기해서 s에 대한 함수식으로 나타낸다.
2. 라플라스 변환의 활용
라플라스변환이 실제로 어떻게 활용되어서 미분방정식을 풀 수 있는지 한번 적용해 보자

위와 같이 초기값이 주어진 2계 비제차 미분방정식이 있다. 이전의 방법으로는 제차해를 먼저 정의하고 결정한 제차해를 통해 비제차해를 구해서 최종 일반해를 결정한다. 그다음 최종적으로 초기값을 대입하여 특수해를 결정했다. 하지만 이식을 라플라스 변환을 하면 다음과 같다.

라플라스 변환결과식은 y에 대한 미분항(y', y'')이 존재하지 않는다. 즉, y에 대해서 정리가 가능한 식으로 만들어졌다. 이식을 y에 대해서 정리하면

이렇게 부분분수 형태로 식이 나타난다. 부분분수로 나타낸 이유는 이형태가 라플라스 역변환(inverse laplace transform) 이 가장 쉬운 형태이기 때문이다. 따라서 이 식을 다시 t에 대한 식(y(t))로 바꾸어주기 위해 역변환을 취해주면 다음과 같이 결과식이 나온다.

이처럼 이전에 소개했던 방법과 비교했을 때 훨씬 간단히 특수해가 나온 것을 확인할 수 있다. 특히 s에 대한 변환식이 y에 미분항을 포함하지 않는다는 점을 이용해서 라플라스 변환과 역변환을 이용해 미분방정식을 풀이하는 메커니즘은 공학에서 상당히 중요하다.
3. 라플라스변환의 선형성
라플라스 연산은 선형연산이다. 즉, 라플라스연산자를 사용한 연산은 선형 시스템에서 모순 없이 성립한다. 수학적으로 라플라스 변환이 존재하는 f(t), g(t)에 대해서 어떤 상수 a, b에 대해서 다음식이 성립한다.

위와 같은 선형성을 이용해서 복잡한 연산식을 보다 간단하게 만들어서 해결하는 경우도 간혹 있으므로 라플라스 연산자의 선형성은 꼭 인지해두자.
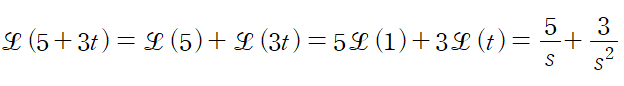
'전공 > 공학수학' 카테고리의 다른 글
| [공학수학1] Laplace Transform (3)-unit step function/unit impulse function (2) | 2023.01.07 |
|---|---|
| [공학수학1] Laplace Transform (2)-제 1이동정리 (0) | 2023.01.07 |
| [공학수학1] 2계 비제차상미분방정식 (2)-매개변수법 (0) | 2023.01.06 |
| [공학수학1] 2계 비제차상미분방정식 (1)-미정계수법 (0) | 2023.01.06 |
| [공학수학1] 2계 제차상미분방정식(3)-오일러 코시 방정식 (0) | 2023.01.05 |



