이번에는 변수분리법이 아닌 다른 방법으로 상미분방정식을 풀이할 수 있는 방법을 살펴보자.
전미분의 형태로 나타난 식을 완전상미분 방정식이라고 한다.

위와 같이 ~dx+~dy=0으로 나타난 형태의 식을 완전상미분방정식이라고 하며, 이러한 형태로 나타난 방정식은 변수분리법이 아닌 전미분의 개념을 이용해서 좀 더 쉽게 미분방정식을 풀이할 수 있다.
1. 전미분의 개념
다변수함수에서 하나의 변수가 변할때의 변화량을 고려하는 것은 편미분이다. 하지만 다변수함수를 모든 변수에 대해서 미분하고 싶다면 편미분을 사용하는 것이 아닌 전미분을 사용해야 한다. 즉, 다변수함수에서 모든 변수에 대한 변화량을 모두 고려하는 것이 전미분의 개념이다.

위와 같이 각각의 변수에 대한 편미분을 구한뒤 더하는 것이 전미분의 정의이다. 이러한 정의를 이용해 완전상미분방정식을 풀 수 있다. 완전상미분방정식 형태에서 p(x)가 x에 대한 편도함수이고, q(y)가 y에 대한 편도함수일 경우에 주어진 미분방정식은 전미분의 형태를 가진다. 따라서 df(x, y)=0의 이므로 주어진 2 변수함수를 적분하면 f(x, y)=c로 상수함수가 된다는 것을 알 수 있다. 상수를 넘겨서 x, y에 대한 관계식을 찾는 것이 미분방정식의 해가 된다.
2. 전미분을 이용한 완전상미분방정식의 풀이
다음의 예제를 한번 풀어보자


(Step 1) 완전미분방정식인지 확인
완전미분방정식이 되기 위한 필요충분조은 다음과 같다.
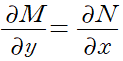
따라서 위의 관계가 성립한다면 완전상미분방정식으로 간주하고 문제를 바로 풀 수 있다.
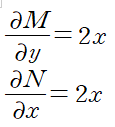
주어진 예제에서는 편도함수가 동일하므로, 주어진 식은 완전상미분방정식임을 알 수 있다.
(Step 2) 전미분의 공식적용
전미분의 정의를 이용해 주어진 식을 적분하면 원함수를 추정할 수 있다.

여기서 주의할 점은 적분을 편적분을 수행하기 때문에 적분상수가 더 이상 상수가 아닌 y에 대한 함수식으로 나오는 것을 주의하자
(Step 3) 나머지식을 이용해 k(y)를 구한다


따라서 주어진 k(y)의 식은 상수항이 된다는것을 식을 통해서 알 수 있다.
결론적으로 미분방정식의 해는 다음과 같이 나온다는것을 알 수 있다.

'전공 > 공학수학' 카테고리의 다른 글
| [공학수학1] 2계 제차상미분방정식(2) (0) | 2023.01.05 |
|---|---|
| [공학수학1] 2계 제차상미분방정식(1) (0) | 2023.01.05 |
| [공학수학1] 1계 상미분방정식(3) (0) | 2023.01.04 |
| [공학수학1] 1계 상미분방정식(1) (0) | 2023.01.03 |
| [공학수학1] 미분방정식의 소개 (0) | 2023.01.03 |



