이전에는 도핑에 대한 캐리어 농도특성을 살펴보았는데 이번에는 캐리어들이 어떤 방법으로 전류를 만들어내는지 한번 알아보자. 특히 이러한 캐리어들의 움직임으로 드리프트 전류가 생성되는 과정을 직접 알아보고 어떤 특성을 갖고 있는지 확인해 보자.
드리프트전류의 개념을 알기 위해서는 드리프트의 개념부터 알아야 한다. 드리프트는 전기장에 의해서 전하가 움직이는 것을 의미한다. 즉 드리프트전류는 전기장에 의해서 캐리어가 움직이면서 생기는 전류이라는 것을 꼭 기억해 두자.
실제적으로 입자의 크기는 매우 작기 때문에 움직임을 식으로 기술하기 쉽지 않다. 특히 전자의 같은 경우에는 전자 하나하나에 대해서 속도를 모두 측정한 뒤에 적분하면 전체 면적에 대해서 전류량을 알 수 있지만, 실질적으로 전자 하나하나에 대해서 속도를 모두 측정할 수는 없기 때문에 평균의 개념을 도입해서 간략화할 수 있다. 특히 진공상태라고 가정하더라도 실제로는 더 많은 여러 가지 입자들이 존재하기 때문에 움직임이 진공과는 다르다는 것을 꼭 인지할 수 있도록 하자.

전자가 매우 많고 위와 같이 모든 전자에대해서 속도를 정의할 수 없기 때문에 평균 드리프트속도라는 개념을 정의해서 식을 정리할 수 있다. 따라서 드리프트 전류식은 다음과 같이 나타난다.

위와 같이 전하밀도와 평균 드리프트 속도의 곱으로 나타난다. 전하의 개념을 캐리어로 확장시키면 자유전자에 대한 식과 양공에 대한 2가지 식이 도출된다. 따라서 다음과 같이 식이 나타난다.

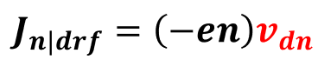
따라서 체적전하밀도가 전하량과 캐리어농도의 곱으로 나타난 것을 확인할 수 있다. 하지만 이 식을 좀 더 바꿀필요가 있다. 왜냐하면 우리는 평균속도를 이용하는 것이 아닌 전기장에 의한 식으로 나타내어야 전기장에 의한 식으로 좀 더 쉽게 해석할 수 있을 것이다. 따라서 평균드리프트속도와 전기장의 관계식을 정의하기 위해서 모빌리티라는 개념을 도입한다. 모빌리티에 대해서 간단히 설명하자면 어떤 캐리어가 전기장에 영향을 받는 정도라고 설명하겠다. 따라서 모빌리티의 값은 물질마다 다르고 값이 클수록 전기장의 영향을 크게 받아 전류가 좀 더 잘 흐를 수 있게 된다. 이때 전기장이 걸리면 단순히 힘을 받는 것이 아닌 입자의 운동경로자체에 힘이 걸리기 때문에 scattering 메커니즘에 의해서 입자가 운동하게 된다. 따라서 다음과 같이 운동한다
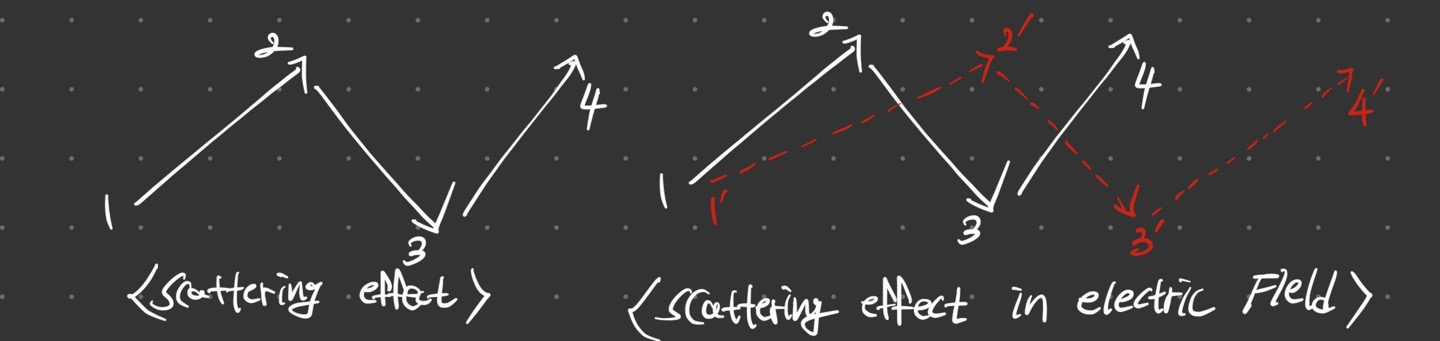
전기장이 걸리게 되면 위와 같이 입자의 이동에 자체에 변화가 생기게 되면서 입자의 최종위치가 변화한다. 하지만 이 입자의 운동은 실제적으로 매우 빠르기 때문에 우리가 관측하는 지점은 오직 4와 4`이며 이 위치변화를 토대로 입자가 힘을 받는 다고 인지하게 된다. 이러한 scattering 메커니즘에 의해서 모빌리티와 전기장의 관계식을 다음과 같이 정의할 수 있다.


관계식이 마찬가지로 양공에서와 자유전자에서 식이 다르게 나타나는 것을 확인할 수 있다. 특히 자유전자식에서는 -부호가 붙어서 반대방향으로 전기장의 영향을 받는다는 사실을 알 수 있다. 왜냐하면 전자의 이동방향은 전기장의 방향과 반대방향이기 때문이다.(전자는 전기장방향에 반대되는 힘을 받기 때문) 따라서 이 관계식을 이용해 최종식을 정리해 보면

위와 같이 모빌리티를 이용해 식이 나타난다. 따라서 총 드리프트전류는 양공과 전자에 의한 드리프트전류식을 모두 더한 것이 되므로 다음과 같이 식이 정의된다.

#Induced electric field
전기장이 생길때 각각의 캐리어는 전기장의 영향을 받아 드리프트전류를 생성한다는 것을 배웠다. 하지만 전기장이 생길 때 에너지 밴드의 구조는 어떻게 될까? 결론부터 말하자면 전기장이 걸린 만큼 에너지밴드는 기울어진다. 즉 반도체에 더 센 전기장이 걸릴수록 밴드의 기울기는 더 급하게 형성된다.

따라서 이것을 식으로 나타내면 다음과 같다.


밴드의 기울기가 곧 전기장의 세기이므로 위와같은 식이 형성된다. 특히 이식은 아인슈타인 관계식을 유도할 때 사용되는 전기장 식이므로 꼭 이해하고 넘어갈 수 있도록 하자. 그리고 자연상태에는 항상 페르미에너지 준위가 상수이므로 다음과 같은 식 역시 성립하게 된다.

밴드의 기울기가 상수이면 linear하다는 것이고 이는 밴드기울기를 상수값으로 지정할 수 있다는 것과 동일하다. 특히 이 개념은 pn접합에서 매우 유용하게 사용되는 개념이고 가장 기본이 되는 개념이기 때문에 꼭 기억해 두자.
'전공 > 물리전자' 카테고리의 다른 글
| [물리전자] 아인슈타인 관계식 (The Einstein Relation) (0) | 2023.02.16 |
|---|---|
| [물리전자] 확산전류 (Diffusion Current) (0) | 2023.02.16 |
| [물리전자] 도핑에 따른 농도특성(Statistics of Donors and Acceptors) (2) (0) | 2023.02.04 |
| [물리전자] 도핑에 따른 농도특성(Statistics of Donors and Acceptors) (0) | 2023.02.02 |
| [물리전자] 도핑캐리어 농도(The extrinsic Carrier Concentration) (0) | 2023.02.01 |



