이전에는 전기장에 의해서 입자들이 힘을 받아서 전류가 발생하는 드리프트 전류에 대해서 알아보았지만 이번에는 확산에 의해서 입자의 이동이 생기는 확산전류에 대해서 알아보자. 확산이라는 것은 알다시피 입자의 농도차이로 인해 입자가 고농도에서 저농도로 이동하는 현상을 확산이라고 정의한다. 이러한 확산의 현상은 반도체에서도 예외 없이 발생하게 된다. 특히 접합부에서의 농도차이로 인해 확산전류가 발생하게 되며 농도차이가 클수록 당연히 더 큰 전류가 발생하게 된다.

이제 확산전류의 공식을 1차원 상의 그래프상에서 flux양으로 전류식을 한번 유도해 보자(1차원선상에서 모델링)

위와 같이 1차 원상에서의 위치에 따른 전자가 linear 하게 분포하고 있다고 가정하자. 만약 x=0 지점에서 flux의 양을 식으로 나타낼 수 있을 것이다.

다음과 같이 x=0 평면을 통과하는 플럭스가 2가지가 있다고 가정해 보자 오른쪽으로 통과하는 플럭스가 있을 것이고 반대로 왼쪽으로 통과하는 플럭스가 있을 것이다.

확산법칙인 픽의 법칙에 의해 전자의 평균열속도 Vth와 전자농도식을 이용해 각각의 flux를 식으로 위와 같이 나타낼 수 있다. 따라서 x=0 평면에 적용되는 총 flux의 양을 구하면 다음과 같다.
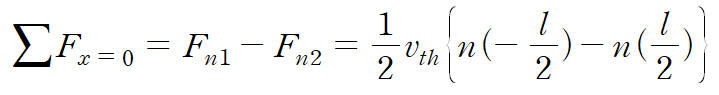
두 플럭스의 방향이 다르기 때문에 단순히 더하는 것이 아닌 방향을 고려해서 벡터합을 이용한다. 이제 좀 더 의미 있는 식을 유도하기 위해서 미분의 정의를 식에 이용해 보자.


미분의 정의를 이용해 중점포인트에서 미분식으로 나타낼 수 있다. 이 식에서 x증분과 y증분이 매우 작다고 가정하면 다음과 같은 미분식으로 보다 정확한 식이 도출된다.

따라서 최종식은 x증분을 0에 가까이 보내면 우리가 알고 있는 미분식으로 변형되면서 다음과 같이 미분항으로 변형된다.


전자와 양 공모도 확산방향은 고농도에서 저농도로 확산되는 것을 알 수 있다. 하지만 +전하인 양공의 확산전류방향은 확산방향과 일치하지만 -전하인 자유전자의 확산전류방향은 확산방향과 반대방향인 것을 확인할 수 있다. 따라서 식에서도 두 캐리어에 의한 식의 부호가 다른 것을 인지하자.
따라서 전류밀도의 정의를 이용해 전자의 선속식을 전하량과 곱해서 다음과 같이 양공과 전자의 확산전류식을 유도할 수 있다.
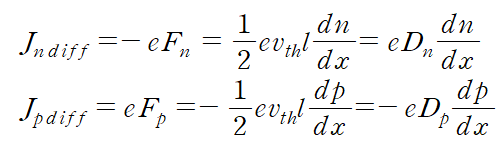
다음과 같이 최종적으로 확산전류식이 유도된다. 식에 최종적으로 사용된 D는 확산계수이고, 이 계수값이 클수록 더 확산이 잘 발생한다는 것을 의미한다. 따라서 앞서 설명한 드리프트전류와 확산전류를 더하면 총전류를 알 수 있다.

위와 같이 드리프트전류와 확산전류식을 더해서 총 토털전류밀도식을 구할 수 있다. 마지막 항은 방향에 의해서 부호가 -부호가 붙는다는 것을 꼭 인지할 수 있도록 하자.
'전공 > 물리전자' 카테고리의 다른 글
| [물리전자] 캐리어의 생성과 소멸 (Carrier generation and recombination) (0) | 2023.02.16 |
|---|---|
| [물리전자] 아인슈타인 관계식 (The Einstein Relation) (0) | 2023.02.16 |
| [물리전자] 표류전류밀도(Drift Current Density) (0) | 2023.02.15 |
| [물리전자] 도핑에 따른 농도특성(Statistics of Donors and Acceptors) (2) (0) | 2023.02.04 |
| [물리전자] 도핑에 따른 농도특성(Statistics of Donors and Acceptors) (0) | 2023.02.02 |



