저번에는 중성영역에서 빌트인 볼티지를 구했고 어떻게 밴드를 형성하는지 알아보았다. 이번에는 중성영역의 전하들에 의해서 생기는 전기장을 직접 유도해 보고 유도된 전기장이 어떤 전위를 유도하는지 알아보자.
#전기장의 유도

저번에 설명했듯이 중성영역에는 전하가 존재하고 양쪽으로 분극된 전하들에 의해서 전기장이 생겨서 드리프트전류와 확산전류가 상쇄되어서 중성상태가 유지된다고 설명하였다. 이번에는 보다 정확한 전하의 분포를 그래프로 한번 살펴보자. 위와 같이 전하가 p영역과 n영역에 일정하게 분포해 있다고 가정하자. 실제로는 위와 같이 이상적으로 분포해 있지는 않지만 전기장을 유도하기 위해서 이상적인 분포를 가정해 보자.

전기장의 유도는 포아송 방정식을 이용해서 전기장을 유도한다. 전하를 미리 가정했기 때문에 포아송 방정식을 적분한뒤 전기장에 대해서 식을 정리하면 전기장식을 알 수 있다. 중성영역에서 경계를 기준으로 왼쪽은 -전하이고 오른쪽은 +전하이므로 x=0을 기준으로 구간을 나누어서 적분을 수행한다. 특히 각각의 경계 x=-xp, x=xn에서 전하는 존재하지 않기 때문에 전기장은 0이어야 하므로 경계조건을 적용해서 적분상수를 쉽게 구할 수 있을 것이다. 따라서 빨간색으로 표시된 부분이 구간별로 구한 최종 전기장의 식이다.

구한 전기장의 식으로 그래프를 그려보면 다음과 같다. 식에서부터 예측할수있는데 1차 함수의 합성으로 이루어져 있다. 그래프를 잘 살펴보면 x=0의 경계에서 연속으로 이루어져 있다는 것을 확인할 수 있다. 당연하게도 경계에서 전기장은 급격하게 변할 수 없기 때문에 연속으로 존재해야 한다. 따라서 이 연속조건까지 이용하면 다음의 식을 얻을 수 있다.


전기장이 x=0에서 연속이라는 조건을 이용하면 위와 같이 도핑농도와 각 영역의 길이를 곱한 값은 항상 같아야 한다는 식이 나오게 된다. 따라서 이 식을 이용해 도핑값이 큰 쪽의 영역이 더 길이가 작아지게 된다는 사실을 예측할 수 있을 것이다.
#퍼텐셜 유도
이번에는 전위식을 한번 유도해 보자. 전위식은 전기장을 적분해서 구할 수 있다. 앞서 구한 전기장의 식을 적분해서 부호를 반대로 한 것이 전위이다.

위와 같이 동일한 방법으로 구간을 나누어서 적분을 수행하면 x에대한 2차식의 형태로 적분결과식이 나오게 된다. 적분상수는 경계조건을 이용해서 결정하는데, 전위는 절대치가 아니라 상대치이기 때문에 어디를 기준으로 설정해도 문제가 없다는 특성이 있다. 따라서 x=-xp일때 전위를 0으로 두면 이것이 결국 경계조건이 된다. 그리고 전위는 x=0의 경계에서 연속이어야 하므로 오른쪽 구간에서의 상수값또한 연속조건을 이용해서 적분상수를 결정할수있다. 따라서 각 구간별 전위를 구할수있다.
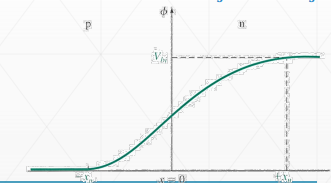
따라서 구간별 전위를 그래프로 나타내면 위와같이 2차 함수의 합성형태로 나타난다. 양 전위차는 결국 빌트인 퍼텐셜로 된다는 것을 주목하자. 따라서 오른쪽구간의 전위 최댓값과 왼쪽 전위의 최솟값의 차이는 항상 빌트인 퍼텐셜로 된다. 왜냐하면 밴드가 휘어진 높이가 결국 전위장벽이 되고, 이 전위장벽이 결국 함숫값의 차이기 때문이다.
#공식유도
앞서 설명한 빌트인 포텐셜 식과 전기장 연속조건식을 연립하면 공식을 유도할 수 있다.

위 두식을 연립하면 중성영역의 각 영역별 길이를 공식으로 유도할수있다. 두 길이를 더하면 중성영역의 총길이가 되므로 이 역시 공식으로 유도가능하다.

'전공 > 물리전자' 카테고리의 다른 글
| [물리전자] 순방향전압(Forward Vias) (0) | 2023.02.22 |
|---|---|
| [물리전자] 역방향전압(Reverse Vias) (0) | 2023.02.21 |
| [물리전자] PN 접합 (PN junction) (1) (1) | 2023.02.20 |
| [물리전자] 앰바이폴라 전송방정식(Ambipolar Transport Equations) (0) | 2023.02.20 |
| [물리전자] 연속방정식(Continuity Equations) (0) | 2023.02.20 |



