이제는 물리량에 따라서 캐리어의 유입과 유출에 관한 식을 한번 유도해 보자. 이 식은 반도체내의 전하의 유입/유출에 대한 식을 유도하는 과정이므로 엠바이폴라 방정식의 기초가 되는 방정식이다. 먼저 1차원운동에서 간단하게 모델링해보자.

위의 그림은 x방향으로의 유입과 유출만을 고려한 모델이다. 이 방향에서 유입량과 유출양의 차이를 알면 미소체적내의 입자가 얼마나 존재하는지 알 수 있을 것이다. 따라서 초기 점화식은 다음과 같이 세워진다.


미분항이 있어서 초기에 이해가 바로 안될수 있지만 결국 증분항을 기울기의 개념을 이용해서 미소 구간을 정의하는 미분항으로 나타낸 것뿐이다.


위 식을 다음과 같이 다시 풀이해볼수있다. 앞서 설명한 대로 유입량에서 유출양을 뺀 값이 현재 미소체적에 존재하는 입자의 양이 되므로 식이 위와 같이 작성된다. 그 후에 미분의 정의를 이용해서 미분항으로 식을 나타낸다.


하지만 이 식은 생성과 소멸을 고려하지 않은 식이므로 생성과 재결합을 고려한 항까지 모두 더해준다. 좌변은 현재 존재하는 입자량이므로 생성되는항은 더해주고 소멸항은 빼주어서 우변을 다시 결정한다. 특히 소멸항에서는 캐리어 life time이 들어가는 것을 확인하자. 이 식은 각각 전자와 홀에 대해서 다시 정리해 보면 다음과 같다. 미소체적인자를 모두 소거하고 x방향만을 남겨서 1차원운동이라고 가정할 때 아래와 같이 식이 x방향만 남게 된다.

이전에 배웠던 드리프트 전류와 확산전류의 식을 이용해서 위 식을 좀 더 활용가능한 식의 형태로 한번 바꿔보자.
#Time Dependent Diffusion Equations
이전에 배웠던 전류식을 다시 떠올려보자.

이식을 이용해 flux의 관계식을 한번 생각해보자.
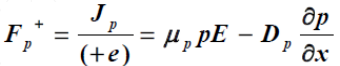
이 관계식을 이용해서 앞서 유도했던 연속방정식에 대입하면 다음과 같다.

따라서 주어진 식을 대입한뒤 정리하면 다음과 같이 식이 나오게 된다.

최종적으로 위 식이 시간과 위치에 대한 과잉 캐리어의 연속방정식이며 이 식을 기초로 앰바이폴라 방정식이유도된다. 이 식은 hole에 대해서 정리한 식이고 전자에 대한 식은 유도방법은 동일하나 식은 약간 다르다. 따라서 최종적으로 전자와 양공에 대한 연속방정식 식은 다음과 같이 결정된다.

위 방정식의 해를 구하면 과잉캐리어의 분포에 대한 식을 얻을 수 있다. 하지만 이 식을 푸는 것은 매우 어렵고 시간과 공간변수가 모두 존재하기 때문에 일반적으로 하나의 축을 고정하고 방정식을 풀어서 문제를 일반화한다. 이 식이 정리되어서 결국 엠바이폴라 방정식이 만들어지는 것이므로 꼭 이해할 수 있도록 하자.
'전공 > 물리전자' 카테고리의 다른 글
| [물리전자] PN 접합 (PN junction) (1) (1) | 2023.02.20 |
|---|---|
| [물리전자] 앰바이폴라 전송방정식(Ambipolar Transport Equations) (0) | 2023.02.20 |
| [물리전자] 홀 효과(The Hall Effect) (0) | 2023.02.18 |
| [물리전자] 캐리어의 생성과 소멸 (Carrier generation and recombination) (3) (0) | 2023.02.17 |
| [물리전자] 캐리어의 생성과 소멸 (Carrier generation and recombination) (2) (0) | 2023.02.17 |



