이제 드디어 앰바이폴라 전송방정식에 대해서 배울 수 있는 모든 기반이 만들어진 것 같다. 수식적으로 굉장히 복잡하고 수학적인 개념도 들어가 있기 때문에 1-2번 봐서는 아마 잘 이해할 수 없을 것이다. 따라서 하나의 과정을 계속 원리를 따져가면서 이해하다 보면 어느 순간에 이 방정식에 왜 최종적으로 이렇게 되는지 이해할 수 있을 것이다. 이제 한번 유도해 보자.
먼저 방정식을 유도하기 전에 이 방정식을 유도하기위한 다양한 전제조건들을 먼저 알아보자.
#엠바이폴라 방정식의 전제조건

반도체에 외부전기장이 걸리게되면 전자와 양공은 전기장의 영향을 받아 양극으로 몰리게 된다. 이때 양극으로 몰린 전자와 양공은 자체적으로 반도체내부에 내부전기장을 형성하게 되는데 이 내부전기장에 의해서 외부전기장에 의한 힘의 반대방향으로 전자와 양공에 가해지게 된다. 즉, 내부전기장에 의해서 전자와 양공이 서로 끌어당기는 힘이 발생한다. 따라서 결론적으로 과잉 전자와 과잉 양공이 확산계수와 모빌리티의 값이 이 내부전기장의 영향으로 같은 값을 가진다는 것이 전송방정식의 전제조건이 된다.

위 방정식을 이용해서 적절하게 우리가 풀수있는형태로 바꾸는 것이 이번 목적이다. 위 공식에서 전기장의 항을 우리가 변형할 것이다. 왜냐하면 내부전기장의 영향은 외부전기장에 비해 무시할 수 있는 수준이기 때문이다.


따라서 전기장이 포함되어있는 위 연속방정식에서 노란색 부분을 소거하는 것이 주목적이다. 이 항을 소거하기 위해서는 다음과 같은 3가지 가정이 필요하다. 이 3가지 가정은 엠바이폴라 방정식을 유도하기 위해서 가장 필수적인 조건이므로 꼭 인지하자.

#전기장항을 소거하기 위한 식유도

p타입을 가정하고 소거를 진행하였으나, n타입을경우에도 동일한 방법으로 식을 차례로 소거해서 계수를 간소화해서 상수계수로 취급하는 것이 핵심이다.

각 타입에서 생성과 소멸에 대한 정리식은 위와같이 정리된다. 앞서 전제로 한 조건에 의해서 평형상태의 생성과 소멸은 모두 상쇄되기 때문에 식이 변형된다.


따라서 식을 최종적으로 정리하면 위와같이 엠바이폴라 전송방정식이 유도된다.
#문제상황별 방정식의 변화
-정상상태(steady state)

정상상태일때는 시간에 따라서 캐리어의 변화가 없으므로 시간항에 대한 미분항은 0으로 되어서 보다 풀기 쉬운 형태의 방정식을 변한다.
-균일한 분포(uniform distribution of excess carriers)

캐리어들이 균일한 분포를 하고있다면 위치에 따라 캐리어의 변화가 없다는 의미와 동일하므로 위치 x에 대한 미분항은 모두 0이 되어 풀기 쉬운 형태로 식이 변화한다.
-전기장이 존재하지않을때 (zero Electric field)
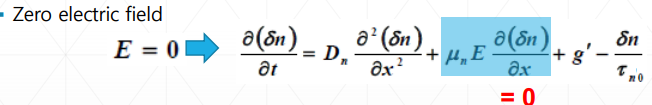
마찬가지로 전기장이 존재하지않을때는 전기장을 포함한 항이 0이 된다.
-생성과 소멸이 0일때
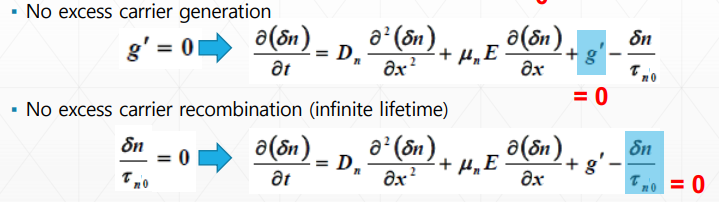
생성과 소멸이 0일 때는 방정식의 상수항이 0이 되면서 미분방정식의 형태가 제차의 형태로 바뀌게 된다. 따라서 생성과 소멸이 0일 때의 상황을 잘 해석해서 식을 간단하게 만드는 것이 중요할 것이다. 문제상황별 식이 어떻게 바뀌는지 잘 숙지해 놓고 문제상황을 잘 파악해서 어떤 항이 0이 되는지 날카롭게 파악해서 미분방정식을 푸는 것이 핵심일 것이다. 문제에서는 직접적으로 언급하지 않은 문제들도 생각보다 많다. 문제를 많이 풀어보고 감을 익히는 것을 추천한다.
'전공 > 물리전자' 카테고리의 다른 글
| [물리전자] PN 접합 (PN junction) (2) (0) | 2023.02.21 |
|---|---|
| [물리전자] PN 접합 (PN junction) (1) (1) | 2023.02.20 |
| [물리전자] 연속방정식(Continuity Equations) (0) | 2023.02.20 |
| [물리전자] 홀 효과(The Hall Effect) (0) | 2023.02.18 |
| [물리전자] 캐리어의 생성과 소멸 (Carrier generation and recombination) (3) (0) | 2023.02.17 |



